Definitions
Ho-Lee model under risk neutral measure:
$$r_{t+\Delta}=r_{t}+\theta_{t}^{*} \Delta+\sigma^{*} \sqrt{\Delta} \varepsilon_{t+\Delta}^{*}$$
$$\varepsilon_{t+\Delta}^{*}=\left\{\begin{array}{l}
+1 \text { with risk neutral probability } 0.5 \\
-1 \text { with risk neutral probability } 0.5
\end{array}\right.$$
- Volatility is constant, which is estimated based on historical data.
- Drift $\theta_t$ is deterministic in the sense that it is not a random variable, but a pure already known function of t.
Graphical illustration of a single step:
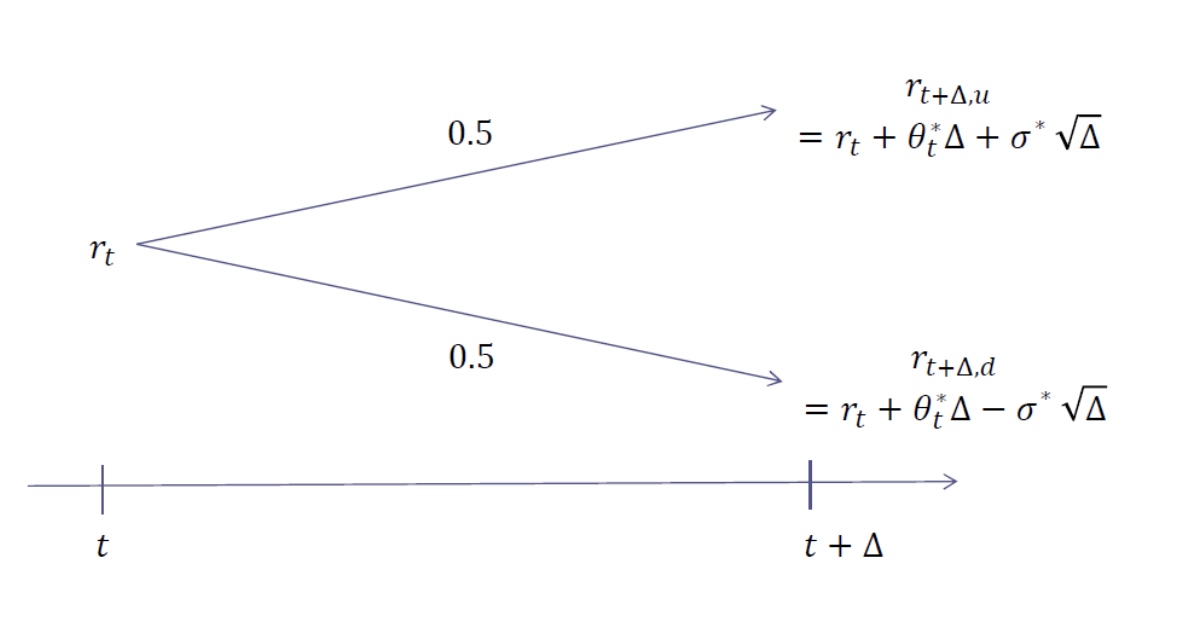
Graphical illustration of two steps:
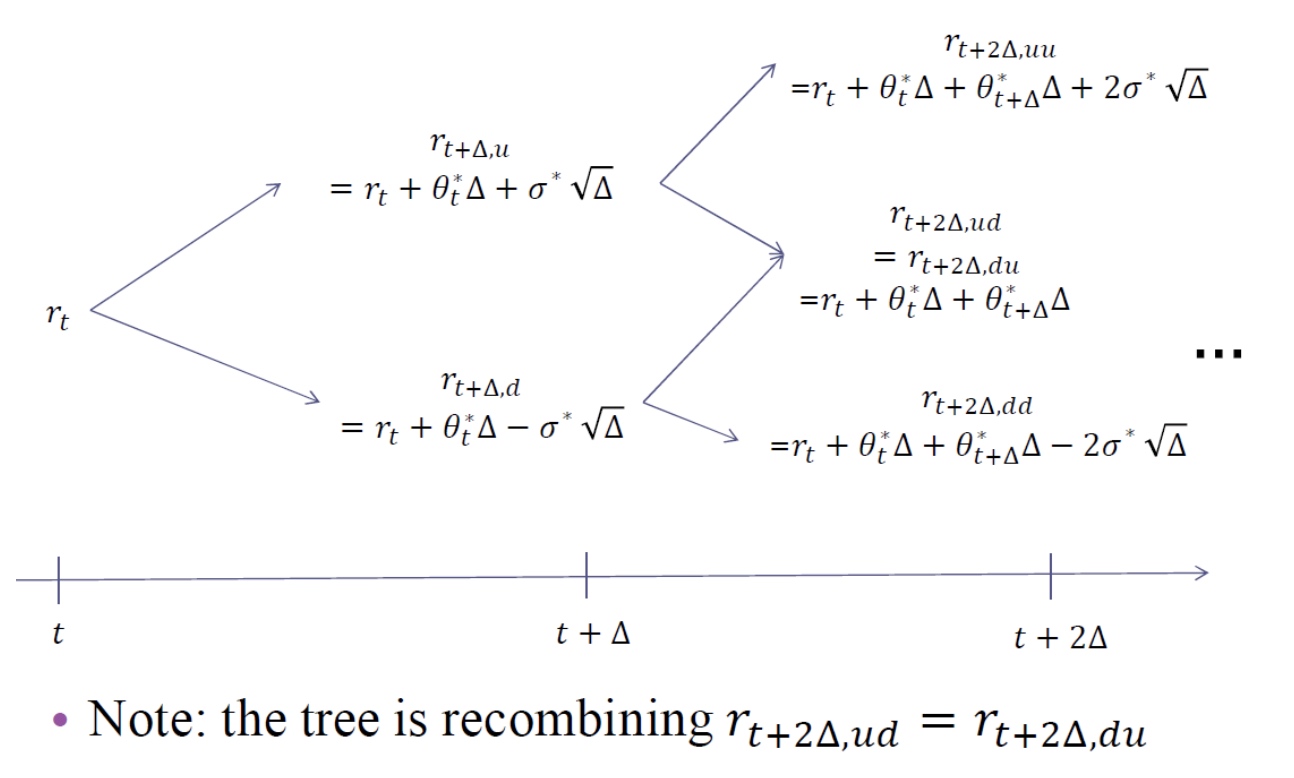
Recombining trees offer numerical tractability
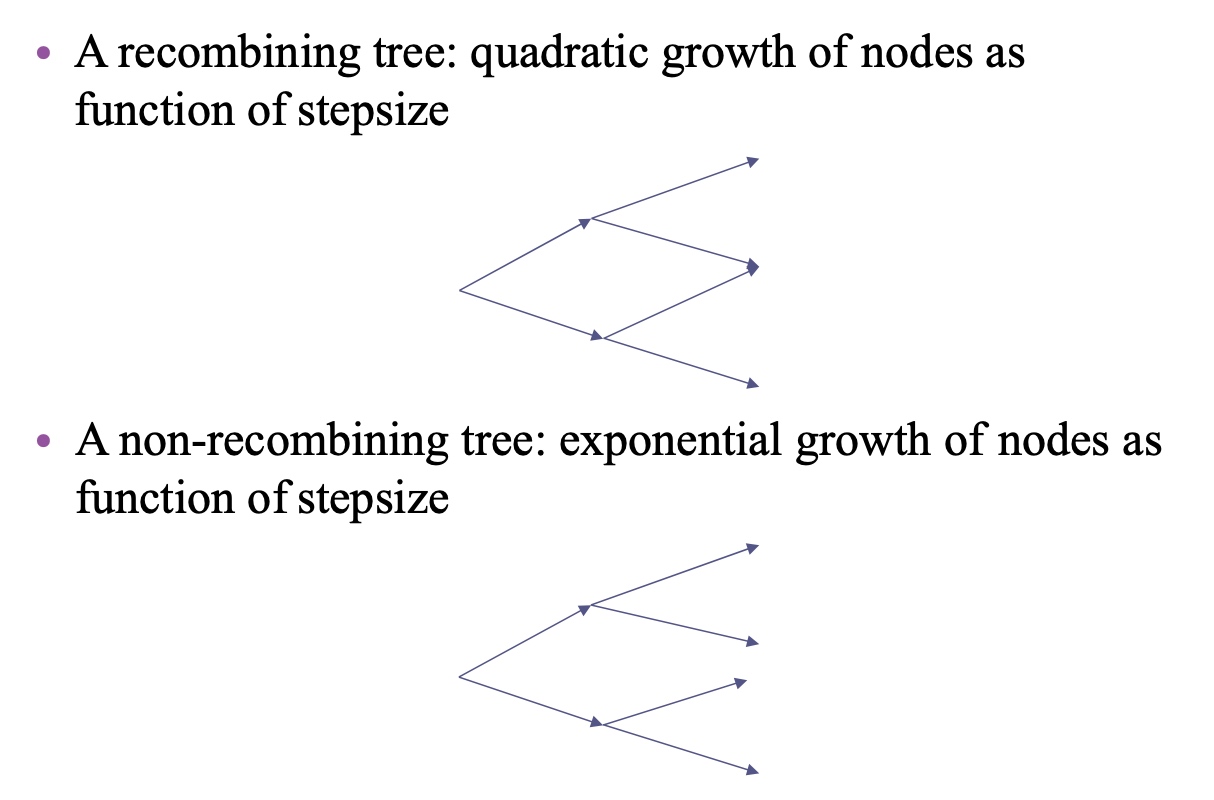
With a fitted Ho-Lee model tree, by risk-neutral pricing:
\[V_0=E_0^Q[\sum_i e^{-(r_o*\Delta+...+r_{i-1}\Delta)} CF_i]\]How to fit the Ho-Lee model
- Start by setting the volatility $\sigma_*$ for interest rate changes.
- This can be estimated from historical data
- Even though we are pricing in the risk-neutral world, the sigma is the same with the physical world.
- Need to pick initial short rate (i.e. $r_0$)
- And One drift parameter (i.e. $\theta^t_*$) for each step
- Pick these parameters so that model implied discount factors agrees with observed discount factors
- Fit the initial term structure in the market.
Assume we already know $r_0$ from observation of $ZCB(0,T_1)$, we price the RN price of $ZCB(0,T_2)$:
\[\begin{aligned} ZCB(0,T_2)&=e^{-r_0 \Delta}E_0^Q(ZCB(T_1,T_2)\\ &=e^{-r_0 \Delta}*(0.5*e^{-r_u \Delta}*1+0.5*e^{-r_d \Delta}*1) \end{aligned}\]Notice that:
\[\begin{aligned} r_{1,u} &=r_0+\theta_0 \Delta + \sigma \sqrt{\Delta}\\ r_{1,d} &=r_0+\theta_0 \Delta - \sigma \sqrt{\Delta}\\ &=r_{1,u}-2 \sigma \sqrt{\Delta} \end{aligned}\]We can fit the $\theta_0$ with $ZCB(0,T_2)$.
Similarly, we can fit the $\theta_1$ with $ZCB(0,T_3)$.
Codes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
"""
Ho Lee Binomial model for Interest Rates
Created by Chen Yangyifan 2021.02.28
"""
class HoLee():
# HoLee Model for pring fixed income products
# P:=[P_1,P_2,...P_T]
# P_i is the the price of zero Coupon Bonds matured in i periods
# Notional Amount is 1
# sigma is the annualized std of short rates in decimals (!!not percentage).
# delta is the time step for each period, e.g. 0.25 year
#########################################################################
#
# Node 0 Node 1 Node 2 Node 3 Node 4 Node 5
#
# 0.066643
# 0.0632758
# 0.0616506 0.0616437
# 0.056084 0.0582758
# 0.05263 0.0566506 0.0566437
#0.04969 0.051084 0.0532758
# 0.04763 0.0516506 0.0516437
# 0.046084 0.0482758
# 0.0466506 0.0466437
# 0.0432758
# 0.04164375
#
##########################################################################
def __init__(self):
import numpy as np
import pandas as pd
self.P_zcb=np.nan
self.sigma=np.nan
self.delta=np.nan
# The risk-neutral Prices Tree
self.prices_tree=np.nan
# The risk-neutral Interest Rates Tree
self.rates_tree=np.nan
self.thetas=np.nan
self.compounding=np.nan
def fit(self,P_zcb,sigma,delta,compounding=0):
# if compounding=0 ,Continuously Compounding
# if compounding=1, compounding 1/delta times a year.
from scipy.optimize import fsolve
import numpy as np
import pandas as pd
thetas=[]
P=list(P_zcb)
if compounding ==0:
r0=np.log(P[0])/(-delta)
else:
r0=(1/P[0]-1)/delta
for i,price in enumerate(P[1:]):
p0=price
func=(lambda t: self.myholee(r0,sigma,delta,thetas+[t],compounding)[0]-p0)
new_theta=fsolve(func,0.02)
thetas.append(new_theta[0])
self.P_zcb=P_zcb
self.sigma=sigma
self.delta=delta
self.thetas=thetas
self.compounding=compounding
self.rates_tree=self.myholee(r0,sigma,delta,thetas,compounding)[2]
self.prices_tree=self.myholee(r0,sigma,delta,thetas,compounding)[1]
return
def summary(self):
print("Fitted Interest Rates Tree:")
print(self.rates_tree)
print("============================")
print("Fitted Prices Tree:")
print(self.prices_tree)
def pricing(self,CFs,type='conditional',defer=1):
import numpy as np
import pandas as pd
def discount(rr,TT):
if self.compounding==0:
return np.exp(-rr*TT)
else:
return 1/(1+rr*self.delta)**(TT/self.delta)
# type: fixed, CFs are fixed, and given as a array [CFS_1,CF_2,...,CF_T]
# type: conditional, CFs are contingent on j,r, and given as a function CFs(j,r)
# defer=0, the contingent CF is paid instantly after the amount is decided
# defer=1, means the contingent CF is paid 1 peirod after the amount is decided.
if type=="fixed":
assert len(CFs)==len(self.P_zcb), "Length of CFs are not equal to Length of Given Zero Coupon Bonds"
prices=np.zeros(self.prices_tree.shape)
layers=prices.shape[1]
for j in np.arange(layers-2,-1,-1):
for i in np.arange(j+1):
r=self.rates_tree.iloc[i,j]
prices[i,j]=discount(r,self.delta)*0.5*(prices[i,j+1]+prices[i+1,j+1])+discount(r,self.delta)*CFs[j]
else:
from inspect import isfunction
assert isfunction(CFs), "For Non-Fixed payoffs, CFs must be a function!"
prices=np.zeros(self.prices_tree.shape)
layers=prices.shape[1]
for j in np.arange(layers-2,-1,-1):
for i in np.arange(j+1):
r=self.rates_tree.iloc[i,j]
# Pay instantly
if defer==0:
prices[i,j]=discount(r,self.delta)*0.5*(prices[i,j+1]+prices[i+1,j+1])+CFs(j,r)
# Pay 1 period after the r is realized
elif defer==1:
prices[i,j]=discount(r,self.delta)*0.5*(prices[i,j+1]+CFs(j,r)+prices[i+1,j+1]+CFs(j,r))
else:
print("defer must be 0 or 1!")
raise Error
return [prices[0,0],pd.DataFrame(prices)]
@staticmethod
def myholee(r0,sigma,delta,thetas,compounding=0):
import numpy as np
import pandas as pd
# r0 is the inital short rate
# thetas are theta_0 to theta_T
# delta is the time step
# m is theta_(T+1)
# compounding: 0: continuously compounding
# compounding: 1: 1/delta times a year
# return P[0,0],Prices, Risk_Neutral_Prices
layers=len(thetas)+1
Prices=np.zeros((layers+1,layers+1))
Prices[:,-1]=np.ones(layers+1)
InterestRates=np.zeros((layers,layers))
def discount(rr,TT):
if compounding==0:
return np.exp(-rr*TT)
else:
return 1/(1+rr*delta)**(TT/delta)
# thetas=thetas+[m]
for j in np.arange(layers-1,-1,-1):
for i in np.arange(j+1):
kk=(j-2*i)*sigma*np.sqrt(delta)
r=r0+np.sum([theta*delta for theta in thetas[:j]])+kk
InterestRates[i,j]=r
Prices[i,j]=0.5*(discount(r,delta)*Prices[i,j+1]+discount(r,delta)*Prices[i+1,j+1])
import pandas as pd
return Prices[0,0],pd.DataFrame(Prices),pd.DataFrame(InterestRates)
if __name__ == "__main__":
hl1 = HoLee()
hl1.summary()
a1 = 1 / (1 + 0.04969 * 0.25) ** 1
a2 = 1 / (1 + 0.04991 * 0.25) ** 2
a3 = 1 / (1 + 0.05030 * 0.25) ** 3
a4 = 1 / (1 + 0.05126 * 0.25) ** 4
a5 = 1 / (1 + 0.05166 * 0.25) ** 5
a6 = 1 / (1 + 0.05207 * 0.25) ** 6
P = [a1, a2, a3, a4, a5, a6]
hl1.fit(P, sigma=0.005, delta=0.25, compounding=1)
hl1.summary()
# Fixed CFs
import numpy as np
CF=2*np.ones(len(P))
print(hl1.pricing(CF,type='fixed')[1])# Price Tree
print(hl1.pricing(CF,type='fixed')[0]) # P_0
print(2*np.sum(P))
# Contigent CFs
hl2=HoLee()
pzcb=[99.1338,97.8925,96.1462,94.1011,91.7136,89.2258,86.8142,84.5016,82.1848,79.7718,77.4339]
pzcb=[item/100 for item in pzcb]
hl2.fit(pzcb,0.0173,0.5)
def mycf(j,r):
# only pays depends on r_10
# max(11*100*r,94)
if j==10:
return max(11*100*r,94)
else:
return 0
mycf(10,0.18856)
p0=hl2.pricing(mycf,type='conditional',defer=0)[0]
print(p0)
price_tree=hl2.pricing(mycf,type='conditional',defer=0)[1]
print(price_tree)
Comments